| Ромбитригексагональная черепица | |
|---|---|
 | |
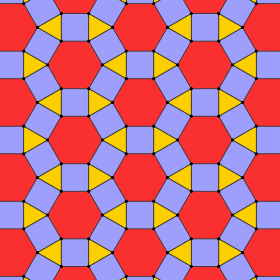| Тип | Полурегулярная черепица |
| Конфигурация вершины |  3.4.6.4 |
| Символ Шлефли | rr {6,3} или |
| Символ Wythoff | 3 | 6 2 |
| Диаграмма Кокстера |     |
| Симметрия | p6m , [6,3], (* 632) |
| Симметрия вращения | п6 , [6,3] + , (632) |
| Акроним Bowers | Ротхат |
| Двойной | Дельтоидальная трехгексагональная черепица |
| Характеристики | Вершинно-транзитивный |
В геометрии , то rhombitrihexagonal черепица является полурегулярно разбиением на евклидовой плоскости . На каждой вершине есть один треугольник , два квадрата и один шестиугольник . Он имеет символ Шлефли rr {3,6}.
Джон Конвей называет это ромбогексаделтилью . [1] Это можно считать cantellated от Нормана Джонсона терминологии или расширенного шестиугольной черепицы по Алисия Буль Стотт оперативного языка «s.
На плоскости 3 правильных и 8 полуправильных мозаик .
Равномерная окраска [ править ]
В ромбитрихексагональной мозаике имеется только одна равномерная раскраска . (Называя цвета индексами вокруг вершины (3.4.6.4): 1232.)
При раскраске ребер существует полусимметричная форма (3 * 3) или орбифолд . Шестиугольники можно рассматривать как усеченные треугольники t {3} с двумя типами ребер. Имеет диаграмму Кокстера 
, Символ Шлефли s 2 {3,6}. Двухцветный квадрат можно преобразовать в равнобедренные трапеции . В пределе, когда прямоугольники вырождаются в ребра, получается треугольная мозаика , построенная как плоскостная треугольная мозаика,.
| Симметрия | [6,3], (* 632) | [6,3 + ], (3 * 3) | ||
|---|---|---|---|---|
| Имя | Ромбитрихексагональный | Кантик курносый треугольный | Курносый треугольный | |
| Изображение | Равномерная окраска лица | Равномерная окраска краев | Неоднородная геометрия | Предел |
| Символ Шлефли | р-р {3,6} | с 2 {3,6} | с {3,6} | |
| Диаграмма Кокстера | | | | |
Примеры [ править ]
Из "Грамматики орнамента" (1856 г.) | Игра Кенсингтон | Напольная плитка, Археологический музей Севильи , Севилья, Испания | Храм Дианы в Ниме, Франция | Римская мозаика на полу в Кастель-ди-Гвидо |
Связанные мозаики [ править ]
Есть одна взаимосвязанная 2-однородная мозаика , состоящая из шестиугольников, разделенных на 6 треугольников. [3] [4]
3.4.6.4 | 3.3.4.3.4 и 3 6 |
Rhombitrihexagonal черепица относится к усеченной trihexagonal плиточные путем замены некоторых из шестиугольников и окружающие квадраты и треугольники с dodecagons:
3.4.6.4 | 4.6.12 |
Упаковка круга [ править ]
Ромбитрихексагональную плитку можно использовать как упаковку кругов , помещая круги равного диаметра в центре каждой точки. Каждый круг находится в контакте с 4 другими кругами в упаковке ( число поцелуев ). [5] Область трансляционной решетки (красный ромб) содержит 6 различных окружностей.
Строительство Wythoff [ править ]
Есть восемь однородных мозаик, которые могут быть основаны на правильном шестиугольном мозаике (или двойном треугольном мозаике ).
Рисуя плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, мы получаем 8 форм, 7 из которых топологически различны. ( Усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные / треугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [6,3], (* 632) | [6,3] + (632) | [6,3 + ] (3 * 3) | |||||||||
| {6,3} | т {6,3} | г {6,3} | т {3,6} | {3,6} | рр {6,3} | tr {6,3} | sr {6,3} | с {3,6} | |||
| | | | | | | | | |||
| 6 3 | 3,12 2 | (3,6) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Униформа двойников | |||||||||||
| V6 3 | Версия 3.12 2 | В (3,6) 2 | V6 3 | V3 6 | V3.4.6.4 | V.4.6.12 | V3 4 .6 | V3 6 | |||
Мутации симметрии [ править ]
Эта мозаика топологически связана как часть последовательности скошенных многогранников с фигурой вершины (3.4.n.4) и продолжается как мозаики гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (* n32) отражательной симметрией .
| * n 32 изменение симметрии расширенных мозаик: 3.4. п. 4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия * n 32 [n, 3] | Сферический | Евклид. | Компактная гиперб. | Paracomp. | ||||
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] ... | * ∞32 [∞, 3] | |
| Фигура | ||||||||
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Дельтоидальная трехгексагональная мозаика [ править ]
| Дельтоидальная трехгексагональная черепица | |
|---|---|
| Тип | Двойной полурегулярный тайлинг |
| Лица | летающий змей |
| Диаграмма Кокстера |  |
| Группа симметрии | p6m, [6,3], (* 632) |
| Группа вращения | п6, [6,3] + , (632) |
| Двойной многогранник | Ромбитригексагональная черепица |
| Конфигурация лица | V3.4.6.4 |
| Характеристики | лицо-переходный |
Deltoidal trihexagonal черепица представляет собой двойной из полурегулярной черепицы , известная как rhombitrihexagonal черепицы. Конвей называет это тетриллом . [1] Края этой мозаики могут быть образованы наложением пересечения правильной треугольной мозаики и шестиугольной мозаики . Каждая грань змея этой плитки имеет углы 120 °, 90 °, 60 ° и 90 °. Это одна из восьми мозаик плоскости, в которой каждое ребро лежит на линии симметрии мозаики. [6]
Deltoidal trihexagonal Черепица является двойным из полурегулярны плиточные rhombitrihexagonal плиточные. [7] Его лица - дельтовидные или воздушные змеи .
Связанные многогранники и мозаики [ править ]
Это один из 7 двойственных однородных мозаик гексагональной симметрии, включая правильные двойственные.
| Симметрия : [6,3], (* 632) | [6,3] + , (632) | |||||
|---|---|---|---|---|---|---|
| V6 3 | Версия 3.12 2 | В (3,6) 2 | V3 6 | V3.4.6.4 | V.4.6.12 | V3 4 .6 |
У этой плитки есть переходные варианты граней , которые могут искажать воздушные змеи в двусторонние трапеции или более общие четырехугольники. Не обращая внимания на цвета лица ниже, полная симметрия - p6m, а нижняя симметрия - p31m с 3 зеркалами, встречающимися в одной точке, и 3-кратными точками вращения. [8]
| Симметрия | p6m, [6,3], (* 632) | p31m, [6,3 + ], (3 * 3) | |
|---|---|---|---|
| Форма | |||
| Лица | летающий змей | Половина правильного шестиугольника | Четырехугольники |
Эта мозаика связана с трехгексагональной мозаикой путем разделения треугольников и шестиугольников на центральные треугольники и объединения соседних треугольников в воздушных змеев.
Deltoidal trihexagonal плиточные является частью набора однородных двойных разбиений, что соответствует двойственной к rhombitrihexagonal черепицей.
Мутации симметрии [ править ]
Этот замощение топологически связано как часть последовательности мозаик с конфигурациями граней V3.4.n.4 и продолжается как мозаики гиперболической плоскости . Эти транзитивные фигуры имеют (* n32) отражательную симметрию .
| Симметрия * n 32 [n, 3] | Сферический | Евклид. | Компактная гиперб. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] ... | * ∞32 [∞, 3] | |
| Рисунок Config. | V3.4.2.4 | V3.4.3.4 | V3.4.4.4 | V3.4.5.4 | V3.4.6.4 | V3.4.7.4 | V3.4.8.4 | V3.4.∞.4 |
Другая дельтовидная (кайт) черепица [ править ]
Возможны другие дельтовидные тилинги.
Точечная симметрия позволяет заполнять плоскость растущими воздушными змеями с топологией в виде квадратной мозаики , V4.4.4.4, и может быть создана путем пересечения струны ловца снов . Ниже приведен пример с двугранной гексагональной симметрией.
Другой переходный тайлинг граней с гранями змеевиков , также топологическая вариация квадратного тайлинга и с конфигурацией граней V4.4.4.4. Он также является вершинно-транзитивным , и каждая вершина содержит все ориентации грани воздушного змея.
| Симметрия | D 6 , [6], (* 66) | pmg, [∞, (2, ∞) + ], (22 *) | p6m, [6,3], (* 632) |
|---|---|---|---|
| Черепица | |||
| Конфигурация | V4.4.4.4 | V6.4.3.4 | |
См. Также [ править ]
 | Викискладе есть медиафайлы по теме " Равномерная мозаика 3-4-6-4" (ромбитрихексагональная мозаика) . |
- Замощения правильных многоугольников
- Список однородных мозаик
Заметки [ править ]
- ^ a b Conway, 2008, таблица p288
- ^ Кольцо циклически изменяет вариацию Jacks Chain
- ^ Chavey, D. (1989). "Тайлинги правильными многоугольниками - II: Каталог мозаик" . Компьютеры и математика с приложениями . 17 : 147–165. DOI : 10.1016 / 0898-1221 (89) 90156-9 .
- ^ "Архивная копия" . Архивировано из оригинала на 2006-09-09 . Проверено 9 сентября 2006 .CS1 maint: заархивированная копия как заголовок ( ссылка )
- ^ Порядок в космосе: исходник по дизайну, Кейт Кричлоу, стр.74-75, образец B
- ^ Кирби, Мэтью; Умбле, Рональд (2011), «Тесселяция краев и головоломки со складыванием штампов», Mathematics Magazine , 84 (4): 283–289, arXiv : 0908.3257 , doi : 10.4169 / math.mag.84.4.283 , MR 2843659 .
- ^ Вайсштейн, Эрик В. «Двойная тесселяция» . MathWorld . (См. Сравнительное наложение этой плитки и ее двойника)
- ^ Плитки и узоры
Ссылки [ править ]
- Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1.(Глава 2.1: Регулярные и однородные мозаики , стр. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X. стр. 40
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1] (Глава 21, Присвоение имен архимедовым и каталонским многогранникам и мозаикам.
- Вайсштейн, Эрик В. "Равномерная мозаика" . MathWorld .
- Вайсштейн, Эрик У. "Полурегулярная тесселяция" . MathWorld .
- Клитцинг, Ричард. «2D евклидовы мозаики x3o6x - rothat - O8» .
- Кейт Кричлоу, Порядок в космосе: справочник по дизайну , 1970, стр. 69-61, Pattern N, Dual p. 77-76, узор 2
- Дейл Сеймур и Джилл Бриттон , Введение в мозаику , 1989, ISBN 978-0866514613 , стр. 50–56, двойная стр. 116
