Golden ratio

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with ${\displaystyle a}$${\displaystyle b}$${\displaystyle a>b>0,}$

where the Greek letter phi (${\displaystyle \varphi }$ or ) represents the golden ratio.^[a] It is an irrational number that is a solution to the quadratic equation with a value of^[2][1]${\displaystyle \phi }$ ${\displaystyle x^{2}-x-1=0,}$

The golden ratio is also called the golden mean or golden section (Latin: sectio aurea).^[3][4] Other names include extreme and mean ratio,^[5] medial section, divine proportion (Latin: proportio divina),^[6] divine section (Latin: sectio divina), golden proportion, golden cut,^[7] and golden number.^[8][9][10]

Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data.^[11] The golden ratio appears in some patterns in nature, including the spiral arrangement of leaves and other plant parts.

Some twentieth-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing this to be aesthetically pleasing. These often appear in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio.

Two quantities and are said to be in the golden ratio if${\displaystyle a}$${\displaystyle b}$ ${\displaystyle \varphi }$

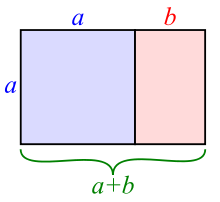
A golden rectangle with long side a and short side b adjacent to a square with sides of length a produces a similar golden rectangle with long side a + b and short side a. This illustrates the relationship ${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi .}$

The Greek letter phi symbolizes the golden ratio. Usually, the lowercase form or is used. Sometimes the uppercase form is used for the reciprocal of the golden ratio, ^[12]${\displaystyle \varphi }$${\displaystyle \phi }$${\displaystyle \Phi }$${\displaystyle 1/\varphi .}$

Michael Maestlin, the first to write a decimal approximation of the ratio

Dan Shechtman demonstrates quasicrystals at the NIST in 1985 using a Zometoy model.

Leonardo's illustration of a dodecahedron from Pacioli's Divina proportione (1509)

Depiction of the proportions in a medieval manuscript. According to Jan Tschichold: "Page proportion 2:3. Margin proportions 1:1:2:3. Text area proportioned in the Golden Section."^[54]

The flag of Togo, whose aspect ratio uses the golden ratio

Detail of the saucer plant, Aeonium tabuliforme, showing the multiple spiral arrangement (parastichy)

If were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the positive integers have a lower bound, so cannot be rational.${\displaystyle \varphi }$${\displaystyle \varphi }$

The golden ratio and its negative reciprocal are the two roots of the quadratic polynomial. The golden ratio's negative and reciprocal are the two roots of the quadratic polynomial .${\displaystyle \varphi }$${\displaystyle -\varphi ^{-1}}$ ${\displaystyle x^{2}-x-1}$${\displaystyle -\varphi }$${\displaystyle \varphi ^{-1}}$${\displaystyle x^{2}+x-1}$

Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers

Approximate and true golden spirals. The green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a Golden Spiral, a special type of logarithmic spiral. Overlapping portions appear yellow. The length of the side of one square divided by that of the next smaller square is the golden ratio.

Dividing a line segment by interior division according to the golden ratio

Dividing a line segment by exterior division according to the golden ratio

Golden triangle. The double-red-arched angle is or radians.${\displaystyle 36^{\circ }}$${\displaystyle {\tfrac {1}{5}}\pi }$

Let and be midpoints of the sides and of an equilateral triangle Extend to meet the circumcircle of at ${\displaystyle A}$${\displaystyle B}$${\displaystyle EF}$${\displaystyle ED}$${\displaystyle DEF.}$${\displaystyle AB}$${\displaystyle DEF}$${\displaystyle C.}$

${\displaystyle {\tfrac {|AB|}{|BC|}}={\tfrac {|AC|}{|AB|}}=\phi }$

A pentagram colored to distinguish its line segments of different lengths. The four lengths are in golden ratio to one another.

The golden ratio in a regular pentagon can be computed using Ptolemy's theorem.

One of the rhombic triacontahedron's rhombi

All of the faces of the rhombic triacontahedron are golden rhombi

A Fibonacci spiral which approximates the golden spiral, using Fibonacci sequence square sizes up to The spiral is drawn starting from the inner square and continues outwards to successively larger squares.${\displaystyle 34.}$${\displaystyle 1\times 1}$

A regular square pyramid is determined by its medial right triangle, whose edges are the pyramid's apothem (),${\displaystyle a}$ semi-base (),${\displaystyle b}$ and height ();${\displaystyle h}$ the face inclination angle is also marked. Mathematical proportions of and and are of particular interest in relation to Egyptian pyramids.${\displaystyle b\mathbin {:} h\mathbin {:} a}$${\displaystyle 1\mathbin {:} {\sqrt {\varphi }}\mathbin {:} \varphi }$${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$${\displaystyle 1\mathbin {:} 4/\pi \mathbin {:} 1.61899}$

The Great Pyramid of Giza

Nautilus shells are often erroneously claimed to be golden-proportioned.

Many of the proportions of the Parthenon are alleged to exhibit the golden ratio, but this has largely been discredited.^[107]

Albert Gleizes, Les Baigneuses (1912)