Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску
Автоморфизм из Клейна четыре группы , показанных как отображение между двумя графами Кэлей , перестановками в обозначениях цикла , а также отображение между двумя столами октав .

В математике , автоморфизм является изоморфизмом из математического объекта к самому себе. В некотором смысле это симметрия объекта и способ сопоставления объекта с самим собой при сохранении всей его структуры. Множество всех автоморфизмов объекта образует группу , называемую группой автоморфизмов . Это, грубо говоря, группа симметрии объекта.

Определение [ править ]

В контексте абстрактной алгебры математический объект - это алгебраическая структура, такая как группа , кольцо или векторное пространство . Автоморфизм просто биективен гомоморфизм объекта с самим собой. (Определение гомоморфизма зависит от типа алгебраической структуры; см., Например, гомоморфизм групп , гомоморфизм колец и линейный оператор ).

Тождественный морфизм ( тождественное отображение ) называется тривиальным автоморфизм в некоторых контекстах. Соответственно, другие (неединичные) автоморфизмы называются нетривиальными автоморфизмами .

Точное определение автоморфизма зависит от типа рассматриваемого «математического объекта» и от того, что именно составляет «изоморфизм» этого объекта. Наиболее общий контекст, в котором эти слова имеют значение, - это абстрактный раздел математики, называемый теорией категорий . Теория категорий имеет дело с абстрактными объектами и морфизмами между этими объектами.

В теории категорий автоморфизм - это эндоморфизм (т. Е. Морфизм объекта в себя), который также является изоморфизмом (в категориальном смысле слова).

Это очень абстрактное определение, поскольку в теории категорий морфизмы не обязательно являются функциями, а объекты не обязательно наборами. Однако в большинстве конкретных настроек объекты будут иметь некоторую дополнительную структуру, а морфизмы будут функциями, сохраняющими эту структуру.

Группа автоморфизмов [ править ]

Основная статья: Группа автоморфизмов

Если автоморфизмы объекта X образует множество (вместо правильного класса ), то они образуют группу в соответствии с составом из морфизмов . Эта группа называется группой автоморфизмов из X .

Закрытие
Другой автоморфизм - это композиция двух автоморфизмов.
Ассоциативность
Часть определения категории состоит в том, что композиция морфизмов ассоциативна.
Личность
Тождество - это морфизм тождества от объекта к самому себе, который является автоморфизмом.
Перевернутые
По определению каждый изоморфизм имеет обратный, который также является изоморфизмом, а поскольку обратный также является эндоморфизмом того же объекта, он является автоморфизмом.

Группа автоморфизмов объекта X в категории C обозначается Aut C ( X ) или просто Aut ( X ), если категория ясна из контекста.

Примеры [ править ]

  • В теории множеств произвольная перестановка элементов множества X является автоморфизмом. Группа автоморфизмов X также называется симметрической группе X .
  • В элементарных арифметиках , множество целых чисел , Z , рассматриваемое как группа по сложению, имеет единственный нетривиальный автоморфизм: отрицание. Однако, рассматриваемое как кольцо, оно имеет только тривиальный автоморфизм. Вообще говоря, отрицание - это автоморфизм любой абелевой группы , но не кольца или поля.
  • Групповой автоморфизм - это групповой изоморфизм группы в себя. Неформально это перестановка элементов группы таким образом, чтобы структура оставалась неизменной. Для каждой группы G существует естественный гомоморфизм групп G → Aut ( G ) , чей образ является группой Inn ( G ) из внутренних автоморфизмов и чье ядро является центром в G . Таким образом, если G имеет тривиальный центр, ее можно вложить в свою группу автоморфизмов. [1]
  • В линейной алгебре , эндоморфизм векторного пространства V является линейным оператором V → V . Автоморфизм является обратимым линейным оператором на V . Когда векторное пространство конечномерно, группа автоморфизмов V совпадает с общей линейной группой GL ( V ). (Алгебраическая структура всех эндоморфизмов V сама по себе является алгеброй над тем же базовым полем, что и V , обратимые элементы которой в точности состоят из GL ( V ).)
  • Поле автоморфизм является биективен кольцевым гомоморфизмом из поля к самому себе. В случаях рациональных чисел ( Q ) и действительных чисел ( R ) нет нетривиальных полевых автоморфизмов. Некоторые подполя в R имеют нетривиальные полевые автоморфизмы, которые, однако, не распространяются на все R (потому что они не могут сохранить свойство числа, имеющего квадратный корень в R ). В случае комплексных чисел , С , существует единственный нетривиальный автоморфизм , что посылает R в R :комплексное сопряжение , но существует бесконечно ( несчетное количество ) «диких» автоморфизмов (если принять аксиому выбора ). [2] [3] Полевые автоморфизмы важны для теории расширений полей , в частности расширений Галуа . В случае расширения Галуа L / K подгруппа всех автоморфизмов L фиксирующих K точечно называется группа Галуа расширения.
  • Группа автоморфизмов кватернионов ( H ) как кольца является внутренними автоморфизмами по теореме Сколема – Нётер : отображения вида a ↦ bab −1 . [4] Эта группа изоморфна с SO (3) , группы вращений в 3-мерном пространстве.
  • Группа автоморфизмов октонионов ( O ) - это исключительная группа Ли G 2 .
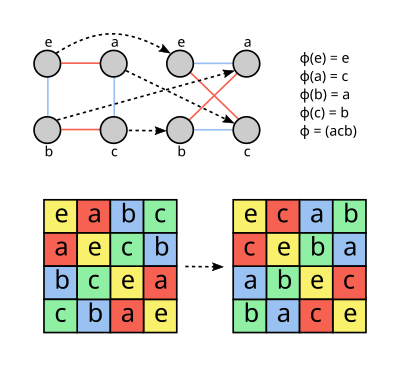
  • В теории графов автоморфизм графа является перестановкой узлов, сохраняющих края и не-ребра. В частности, если два узла соединены ребром, то же самое происходит и с их изображениями при перестановке.
  • В геометрии автоморфизм можно назвать движением пространства. Также используется специализированная терминология:
    • В метрической геометрии автоморфизм - это самоизометрия . Группа автоморфизмов также называется группой изометрий .
    • В категории римановых поверхностей автоморфизм - это биголоморфное отображение (также называемое конформным отображением ) поверхности на себя. Например, автоморфизмы сферы Римана являются преобразованиями Мёбиуса .
    • Автоморфизм дифференцируемого многообразия М является Диффеоморфизмом от М к себе. Группу автоморфизмов иногда обозначают Diff ( M ).
    • В топологии морфизмы между топологическими пространствами называются непрерывными отображениями , а автоморфизм топологического пространства - это гомеоморфизм пространства на себя или самогомеоморфизм (см. Группу гомеоморфизмов ). В этом примере недостаточно, чтобы морфизм был биективным, чтобы быть изоморфизмом.

История [ править ]

Один из самых ранних групповых автоморфизмов (автоморфизм группы, а не просто группы автоморфизмов точек) был дан ирландским математиком Уильямом Роуэном Гамильтоном в 1856 году в его икозиановом исчислении , где он обнаружил автоморфизм второго порядка, [5] написав :

так что это новый пятый корень единства, связанный с прежним пятым корнем отношениями совершенной взаимности.

Внутренний и внешний автоморфизмы [ править ]

Основные статьи: Внутренний автоморфизм и группа внешних автоморфизмов

В некоторых категориях, особенно в группах , кольцах и алгебрах Ли, можно разделить автоморфизмы на два типа, называемые «внутренними» и «внешними» автоморфизмами.

В случае групп внутренние автоморфизмы - это сопряжения элементами самой группы. Для каждого элемента a группы G сопряжение с помощью a - это операция φ a : G → G, заданная формулой φ a ( g ) = aga −1 (или a −1 ga ; использование меняется). Легко проверить, что сопряжение с помощью a является групповым автоморфизмом. Внутренние автоморфизмы образуют нормальную подгруппу в Aut ( G ), обозначаемую Inn ( G ); это называетсяЛемма Гурса .

Остальные автоморфизмы называются внешними автоморфизмами . Фактор - группа Aut ( G ) / Inn ( G ) обычно обозначается Out ( G ); нетривиальные элементы - это смежные классы , содержащие внешние автоморфизмы.

То же определение справедливо для любого кольца с единицей или алгебры, где a - любой обратимый элемент . Для алгебр Ли определение несколько иное.

См. Также [ править ]

  • Антиавтоморфизм
  • Автоморфизм (в головоломках судоку)
  • Характеристическая подгруппа
  • Кольцо эндоморфизмов
  • Автоморфизм Фробениуса
  • Морфизм
  • Автоморфизм порядка (в теории порядка ).
  • Автоморфизм, сохраняющий отношения
  • Дробное преобразование Фурье

Ссылки [ править ]

  1. ^ PJ Пал, R Damrath (2001). «§7.5.5 Автоморфизмы» . Математические основы вычислительной техники (перевод под ред. Феликса Пала). Springer. п. 376. ISBN. 3-540-67995-2.
  2. ↑ Йель, Пол Б. (май 1966 г.). "Автоморфизмы комплексных чисел" (PDF) . Математический журнал . 39 (3): 135–141. DOI : 10.2307 / 2689301 . JSTOR 2689301 .  
  3. ^ Lounesto, Pertti (2001), Клиффорд алгебры и Спиноры (2 - е изд.), Cambridge University Press, стр. 22-23, ISBN 0-521-00551-5
  4. ^ Справочник по алгебре , 3 , Elsevier , 2003, стр. 453
  5. ^ Сэр Уильям Роуэн Гамильтон (1856). «Меморандум о новой системе корней единства» (PDF) . Философский журнал . 12 : 446.

Внешние ссылки [ править ]

  • Автоморфизм в энциклопедии математики
  • Вайсштейн, Эрик В. «Автоморфизм» . MathWorld .