Функция Миттаг-Леффлера

Функцию Миттаг-Леффлера можно использовать для непрерывной интерполяции между гауссовой и лоренцевой функциями.

В математике , то М.-Л. функция Е _{α , β} представляет собой специальную функцию , А комплекс функция , которая зависит от двух комплексных параметров α и бета . Его можно определить следующей серией, когда действительная часть α строго положительна: ^{[1] [2]}

${\ displaystyle E _ {\ alpha, \ beta} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {\ Gamma (\ alpha k + \ beta)}} .}$

где - гамма-функция . Когда это сокращается как . Для получения , серия выше равна разложения в ряд Тейлора геометрической прогрессии , а следовательно .${\ Displaystyle \ Gamma (х)}$${\ displaystyle \ beta = 1}$${\ Displaystyle Е _ {\ альфа} (г) = Е _ {\ альфа, 1} (г)}$${\ Displaystyle \ альфа = 0}$${\ displaystyle E_ {0, \ beta} (z) = {\ frac {1} {\ Gamma (\ beta)}} {\ frac {1} {1-z}}}$

В случае, когда α и β действительны и положительны, ряд сходится для всех значений аргумента z , поэтому функция Миттаг-Леффлера является целой функцией . Эта функция названа в честь Гёста Миттаг-Леффлера . Этот класс функций важен в теории дробного исчисления .

При α  > 0 функция Миттаг-Леффлера является целой функцией порядка 1 / α и в некотором смысле является простейшей целой функцией своего порядка.${\ Displaystyle Е _ {\ альфа, 1} (г)}$

Функция Миттаг-Леффлера удовлетворяет свойству рекуррентности (теорема 5.1 из ^[1] )

${\ Displaystyle E _ {\ alpha, \ beta} (z) = {\ frac {1} {z}} E _ {\ alpha, \ beta - \ alpha} (z) - {\ frac {1} {z \ Gamma (\ бета - \ альфа),}}}$

откуда асимптотическое разложение Пуанкаре

${\ displaystyle E _ {\ alpha, \ beta} (z) \ sim - \ sum _ {k = 1} {\ frac {1} {z ^ {k} \ Gamma (\ beta -k \ alpha)}}}$

следует, что верно для .${\ Displaystyle г \ к - \ infty}$

Особые случаи [ править ]

Ибо находим: (Раздел 2 ^[1] )${\ Displaystyle \ альфа = 0,1 / 2,1,2}$

Функция ошибки :

${\ displaystyle E _ {\ frac {1} {2}} (z) = \ exp (z ^ {2}) \ operatorname {erfc} (-z).}$

Сумма геометрической прогрессии :

${\displaystyle E_{0}(z)=\sum _{k=0}^{\infty }z^{k}={\frac {1}{1-z}},\,|z|<1.}$

Экспоненциальная функция :

${\displaystyle E_{1}(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (k+1)}}=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}=\exp(z).}$

Гиперболический косинус :

${\displaystyle E_{2}(z)=\cosh({\sqrt {z}}),{\text{ and }}E_{2}(-z^{2})=\cos(z).}$

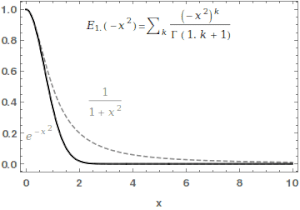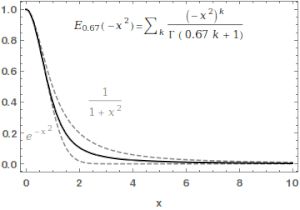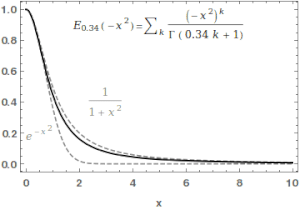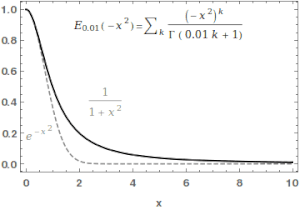
Ибо у нас есть${\displaystyle \beta =2}$

${\displaystyle E_{1,2}(z)={\frac {e^{z}-1}{z}},}$

${\displaystyle E_{2,2}(z)={\frac {\sinh({\sqrt {z}})}{\sqrt {z}}}.}$

В самом деле, интеграл${\displaystyle \alpha =0,1,2}$

${\displaystyle \int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d} }s}$

дает, соответственно: , , .${\displaystyle \arctan(z)}$${\displaystyle {\tfrac {\sqrt {\pi }}{2}}\operatorname {erf} (z)}$${\displaystyle \sin(z)}$

Интегральное представление Миттаг-Леффлера [ править ]

Интегральное представление функции Миттаг-Леффлера (раздел 6 статьи ^[1] )

${\displaystyle E_{\alpha ,\beta }(z)={\frac {1}{2\pi i}}\int _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,}$

где контур C начинается и заканчивается в −∞ и огибает особенности и точки ветвления подынтегрального выражения.

С преобразованием Лапласа и суммированием Миттаг-Леффлера связано выражение (уравнение (7.5) из, ^[1] с m = 0)

${\displaystyle \int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.}$

См. Также [ править ]

• Суммирование Миттаг-Леффлера
• Распределение Mittag-Leffler
• Функция Фокса – Райта

Заметки [ править ]

• Пакет R «MittagLeffleR» от Гуртека Гилла, Питера Страка. Реализует функцию Миттаг-Леффлера, распределение, генерацию случайных переменных и оценку.

Ссылки [ править ]

Эта статья включает в себя список литературы , связанной литературы или внешних ссылок , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Сентябрь 2015 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

• Mittag-Leffler, MG: Sur la nouvelle fonction E (x). CR Acad. Sci. Париж, 137, 554–558 (1903)
• Mittag-Leffler, MG: Sopra la funzione E˛.x /. Ренд. R. Acc. Линчеи, (сер. 5) 13, 3–5 (1904).
• Горенфло Р., Килбас А.А., Майнарди Ф., Рогозин С.В., Функции Миттаг-Леффлера, связанные темы и приложения (Спрингер, Нью-Йорк, 2014) 443 страницы ISBN 978-3-662-43929-6 
• Игорь Подлубный (1998). "глава 1". Дробные дифференциальные уравнения. Введение в дробные производные, дробные дифференциальные уравнения, некоторые методы их решения и некоторые их приложения . Математика в науке и технике. Академическая пресса. ISBN 0-12-558840-2.
• Кай Дитхельм (2010). "Глава 4". Анализ дробных дифференциальных уравнений: прикладное изложение с использованием дифференциальных операторов типа Капуто . Конспект лекций по математике. Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 978-3-642-14573-5.

Внешние ссылки [ править ]

• Справочник по функциям Миттаг-Леффлера по математике mathHandbook.com
• Функция Миттаг-Леффлера: код MATLAB
• Миттаг-Леффлер и стабильные случайные числа: случайные блуждания в непрерывном времени и стохастическое решение уравнений дробной диффузии в пространстве-времени

Эта статья включает материал из функции Mittag-Leffler на PlanetMath , которая находится под лицензией Creative Commons Attribution / Share-Alike License .