| 5-симплексный Hexateron (hix) | ||
|---|---|---|
| Тип | равномерный 5-многогранник | |
| Символ Шлефли | {3 4 } | |
| Диаграмма Кокстера | ||
| 4-гранный | 6 | 6 {3,3,3} |
| Клетки | 15 | 15 {3,3} |
| Лица | 20 | 20 {3} |
| Края | 15 | |
| Вершины | 6 | |
| Фигура вершины | 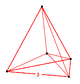 5-элементный | |
| Группа Коксетера | A 5 , [3 4 ], заказ 720 | |
| Двойной | самодвойственный | |
| Базовая точка | (0,0,0,0,0,1) | |
| Circumradius | 0,645497 | |
| Характеристики | выпуклый , изогональный правильный , самодуальный | |
В пятимерной геометрии 5- симплекс - это самодуальный правильный 5-многогранник . У него шесть вершин , 15 ребер , 20 треугольных граней , 15 тетраэдрических ячеек и 6 5-ячеечных граней . Он имеет двугранный угол cos −1 (1/5), или примерно 78,46 °.
5-симплекс - это решение проблемы: сделайте 20 равносторонних треугольников, используя 15 спичек, где каждая сторона каждого треугольника - это ровно одна спичка.
Альтернативные имена [ править ]
Она также может быть названа hexateron или гекс-5-пьянствовать , как 6- фацетного многогранника в 5 измерений. Название hexateron происходит от гекса- за то, что шесть граней и Терон (с тер- будучи порча тетра- ) за то, что четырехмерные грани.
Джонатан Бауэрс дает гексатерону аббревиатуру hix . [1]
Как конфигурация [ править ]
Эта матрица конфигурации представляет собой 5-симплекс. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам и 4-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем 5-симплексе. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного симплекса идентична ее повороту на 180 градусов. [2] [3]
Обычные декартовы координаты гексатерона [ править ]
Hexateron может быть построена из 5-клеток путем добавления 6 - й вершины таким образом, что она находится на одинаковом расстоянии от всех других вершин 5-клетки.
В декартовы координаты для вершин происхождения в центре регулярной hexateron , имеющей длину ребра 2 , являются:
Вершины 5-симплекса проще расположить на гиперплоскости в 6-пространстве как перестановки (0,0,0,0,0,1) или (0,1,1,1,1,1). Эти конструкции можно рассматривать как грани 6-ортоплекса или выпрямленного 6-куба соответственно.
Проецируемые изображения [ править ]
| К плоскости Косетер | А 5 | А 4 |
|---|---|---|
| График | ||
| Двугранная симметрия | [6] | [5] |
| К плоскости Косетер | А 3 | А 2 |
| График | ||
| Двугранная симметрия | [4] | [3] |
Стереографическая проекция 4D-3D диаграммы Шлегеля 5D-4D гексатерона. |
Формы более низкой симметрии [ править ]
Форма более низкой симметрии - это пирамида из 5 ячеек () v {3,3,3} с [3,3,3] порядком симметрии 120, построенная как основание из 5 ячеек в гиперплоскости с 4 пространствами и вершина точка над гиперплоскостью. Пять сторон пирамиды состоят из 5-ти ячеек. Они выглядят как фигуры вершин усеченных правильных 6-многогранников , подобных усеченному 6-кубу .
Другая форма - это {} v {3,3}, с [2,3,3] порядком симметрии 48, соединение ортогонального двуугольника и тетраэдра с ортогональным смещением со всеми парами вершин, соединенными между собой. Другая форма - {3} v {3} с [3,2,3] порядком симметрии 36 и расширенной симметрией [[3,2,3]], порядком 72. Она представляет собой соединение двух ортогональных треугольников, ортогонально смещенных, со всеми парами вершин, соединенными между собой.
Они рассматриваются в цифрах вершинных из bitruncated и tritruncated регулярных 6-многогранников, подобно bitruncated 6-куба и tritruncated 6-симплекс . Метки кромок здесь представляют типы граней в этом направлении и, таким образом, представляют различную длину кромок.
| () v {3,3,3} | {} v {3,3} | {3} v {3} | ||
|---|---|---|---|---|
| усеченный 6-симплексный | усеченный 6-куб | бит-усеченный 6-симплексный | усеченный битом 6-куб | усеченный 6-симплекс |
Соединение [ править ]
На этой проекции плоскости Кокстера A6 можно увидеть соединение двух 5-симплексов в двойных конфигурациях с красными и синими 5-симплексными вершинами и ребрами. Это соединение имеет симметрию [[3,3,3,3]] порядка 1440. Пересечение этих двух 5-симплексов является однородным двунаправленным 5-симплексом .![]()
![]()
![]()
![]()
![]() знак равно
знак равно ![]()
![]()
![]()
![]()
![]() ∩
∩ ![]()
![]()
![]()
![]()
![]() .
.
Связанные однородные 5-многогранники [ править ]
Он является первым в размерном ряду однородных многогранников и сот, выраженном Кокстером как 1 3k рядов. Вырожденный 4-мерный случай существует как разбиение на 3 сферы, тетраэдрический хозоэдр .
| Космос | Конечный | Евклидово | Гиперболический | |||
|---|---|---|---|---|---|---|
| п | 4 | 5 | 6 | 7 | 8 | 9 |
| Группа Коксетера | А 3 А 1 | А 5 | D 6 | E 7 | = E 7 + | = E 7 ++ |
| Диаграмма Кокстера | ||||||
| Симметрия | [3 −1,3,1 ] | [3 0,3,1 ] | [3 1,3,1 ] | [3 2,3,1 ] | [[3 3,3,1 ]] | [3 4,3,1 ] |
| Приказ | 48 | 720 | 23 040 | 2 903 040 | ∞ | |
| График | - | - | ||||
| Имя | 1 3, -1 | 1 30 | 1 31 | 1 32 | 1 33 | 1 34 |
Он является первым в ряду размерностей однородных многогранников и сот, выраженных Кокстером как ряд 3 k1 . Вырожденный 4-мерный случай существует как разбиение на 3 сферы, тетраэдрический диэдр .
| Космос | Конечный | Евклидово | Гиперболический | |||
|---|---|---|---|---|---|---|
| п | 4 | 5 | 6 | 7 | 8 | 9 |
| Группа Коксетера | А 3 А 1 | А 5 | D 6 | E 7 | = E 7 + | = E 7 ++ |
| Диаграмма Кокстера | ||||||
| Симметрия | [3 −1,3,1 ] | [3 0,3,1 ] | [[3 1,3,1 ]] = [4,3,3,3,3] | [3 2,3,1 ] | [3 3,3,1 ] | [3 4,3,1 ] |
| Приказ | 48 | 720 | 46 080 | 2 903 040 | ∞ | |
| График | - | - | ||||
| Имя | 3 1, -1 | 3 10 | 3 11 | 3 21 | 3 31 | 3 41 |
5-симплекс, как многогранник 2 20, является первым в размерном ряду 2 2k .
| Космос | Конечный | Евклидово | Гиперболический | ||
|---|---|---|---|---|---|
| п | 4 | 5 | 6 | 7 | 8 |
| Группа Коксетера | А 2 А 2 | А 5 | E 6 | = E 6 + | E 6 ++ |
| Диаграмма Кокстера | |||||
| График | ∞ | ∞ | |||
| Имя | 2 2, -1 | 2 20 | 2 21 | 2 22 | 2 23 |
Регулярный 5-симплекс является одним из 19 однородных многопланов, основанных на [3,3,3,3] группе Кокстера , все они показаны здесь в ортогональных проекциях A 5 плоскости Кокстера . (Вершины окрашены в соответствии с порядком перекрытия проекций: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый, количество вершин постепенно увеличивается)
| Многогранники A5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
т 0 | т 1 | т 2 | т 0,1 | т 0,2 | т 1,2 | т 0,3 | |||||
т 1,3 | т 0,4 | т 0,1,2 | т 0,1,3 | т 0,2,3 | т 1,2,3 | т 0,1,4 | |||||
т 0,2,4 | т 0,1,2,3 | т 0,1,2,4 | т 0,1,3,4 | т 0,1,2,3,4 | |||||||
Заметки [ править ]
- ^ Клитцинг, Ричард. «5D однородные многогранники (polytera) x3o3o3o3o - hix» .
- ^ Кокстеровские 1973 , пункте 1.8 Конфигурации
- ^ Косетер, HSM (1991). Регулярные сложные многогранники (2-е изд.). Издательство Кембриджского университета. п. 117. ISBN 9780521394901.
Ссылки [ править ]
- Госсет, Т. (1900). «О правильных и полурегулярных фигурах в пространстве n измерений». Вестник математики . Макмиллан. С. 43–.
- Кокстер, HSM :
- - (1973). «Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)». Правильные многогранники (3-е изд.). Дувр. С. 296 . ISBN 0-486-61480-8.
- Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони С .; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные сочинения HSM Coxeter . Вайли. ISBN 978-0-471-01003-6.
- (Документ 22) - (1940). «Правильные и полурегулярные многогранники I» . Математика. Zeit . 46 : 380–407. DOI : 10.1007 / BF01181449 . S2CID 186237114 .
- (Документ 23) - (1985). «Правильные и полурегулярные многогранники II» . Математика. Zeit . 188 (4): 559–591. DOI : 10.1007 / BF01161657 . S2CID 120429557 .
- (Документ 24) - (1988). «Правильные и полурегулярные многогранники III» . Математика. Zeit . 200 : 3–45. DOI : 10.1007 / BF01161745 . S2CID 186237142 .
- Конвей, Джон Х .; Берджел, Хайди; Гудман-Штрасс, Хаим (2008). «26. Hemicubes: 1 n1 ». Симметрии вещей . п. 409. ISBN. 978-1-56881-220-5.
- Джонсон, Норман (1991). «Единые многогранники» (Рукопись). Cite journal requires
|journal=(help)- Джонсон, NW (1966). Теория однородных многогранников и сот (PhD). Университет Торонто.
Внешние ссылки [ править ]
- Ольшевский, Георгий. «Симплекс» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Многогранники разных измерений , Джонатан Бауэрс
- Многомерный глоссарий
| Семья | А п | B n | I 2 (p) / D n | E 6 / E 7 / E 8 / F 4 / G 2 | H n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Правильный многоугольник | Треугольник | Квадрат | п-угольник | Шестиугольник | Пентагон | |||||||
| Равномерный многогранник | Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | ||||||||
| Равномерный 4-многогранник | 5-элементный | 16 ячеек • Тессеракт | Demitesseract | 24-элементный | 120 ячеек • 600 ячеек | |||||||
| Равномерный 5-многогранник | 5-симплекс | 5-ортоплекс • 5-куб. | 5-полукуб | |||||||||
| Равномерный 6-многогранник | 6-симплекс | 6-ортоплекс • 6-куб. | 6-полукуб | 1 22 • 2 21 | ||||||||
| Равномерный 7-многогранник | 7-симплекс | 7-ортоплекс • 7-куб | 7-полукруглый | 1 32 • 2 31 • 3 21 | ||||||||
| Равномерный 8-многогранник | 8-симплекс | 8-ортоплекс • 8-куб | 8-полукруглый | 1 42 • 2 41 • 4 21 | ||||||||
| Равномерный 9-многогранник | 9-симплекс | 9-ортоплекс • 9-куб | 9-полукруглый | |||||||||
| Равномерный 10-многогранник | 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | |||||||||
| Равномерное n - многогранник | n - симплекс | n - ортоплекс • n - куб | n - demicube | 1 к2 • 2 к1 • к 21 | n - пятиугольный многогранник | |||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||

![{\ displaystyle {\ begin {align} & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1) } {\ sqrt {6}}}, \ {\ tfrac {1} {\ sqrt {3}}}, \ \ pm 1 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1} {\ sqrt {6}}}, \ - {\ tfrac {2} {\ sqrt {3}}}, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}} , \ - {\ tfrac {\ sqrt {3}} {\ sqrt {2}}}, \ 0, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15 }}}, \ - {\ tfrac {2 {\ sqrt {2}}} {\ sqrt {5}}}, \ 0, \ 0, \ 0 \ right) \\ [5pt] & \ left (- { \ tfrac {\ sqrt {5}} {\ sqrt {3}}}, \ 0, \ 0, \ 0, \ 0 \ right) \ end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b79141ce810582c49e87824bc8b0f8a7ccec5d90)


