В геометрии , то плотность из звезд многогранника является обобщением понятия обмотки числа от двух измерений до более высоких размеров, представляющее число витков многогранника вокруг центра симметрии многогранника. Его можно определить, пропустив луч из центра в бесконечность, пройдя только через грани многогранника, а не через какие-либо детали более низкой размерности, и посчитав, через сколько граней он проходит. Для многогранников, для которых это количество не зависит от выбора луча и для которых центральная точка не находится на какой-либо грани, плотность задается этим количеством пересеченных граней.
То же самое вычисление можно выполнить для любого выпуклого многогранника , даже без симметрии, выбрав любую точку внутри многогранника в качестве его центра. Для этих многогранников плотность будет равна 1. В более общем случае для любого несамопересекающегося (акоптического) многогранника плотность может быть вычислена как 1 с помощью аналогичного вычисления, при котором выбирается луч из внутренней точки, который проходит только через грани многогранника. многогранник добавляет единицу, когда этот луч проходит изнутри многогранника во внешнюю, и вычитает единицу, когда этот луч проходит из внешней части во внутреннюю часть многогранника. Однако такое присвоение знаков пересечениям обычно не относится к звездным многогранникам, поскольку они не имеют четко определенного внутреннего и внешнего вида.
Тесселяции с перекрывающимися гранями могут точно так же определять плотность как количество покрытий граней в любой заданной точке. [1]
Полигоны [ править ]
Плотность многоугольника есть число раз , что ломаная граница огибает его центр. Для выпуклых многоугольников и, в более общем смысле, простых многоугольников (не самопересекающихся) плотность равна 1 по теореме Жордановой кривой .
Плотность многоугольника также можно назвать его числом поворота ; сумма углов поворота всех вершин, деленная на 360 °. Это будет целое число для всех уникурсальных путей на плоскости.
Плотность составного многоугольника - это сумма плотностей составляющих многоугольников.
Правильные звездчатые многоугольники [ править ]
Для правильного звездного многоугольника { p / q } плотность равна q . Его можно визуально определить, посчитав минимальное количество пересечений краев луча от центра до бесконечности.
Примеры [ править ]
Многоугольник с одинарным пересечением, как этот равносторонний пятиугольник , имеет плотность 0.
Правильный пятиугольник {5} имеет плотность 1.
Изотоксальный тетрадекагон , {(7/2) α }, имеет плотность 2, как и обычный {7/2}.
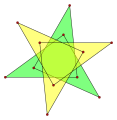
Гептаграмма {7/3} имеет плотность 3.
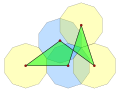
Изотоксальная гексаграмма (соединение) 2 {(3/2) α } имеет плотность 4.
Изотоксальная додекаграмма {(6/5) α } имеет плотность 5, аналогичную обычной {12/5}.
Многогранники [ править ]
Многогранник и двойник к нему имеют одинаковую плотность.
Полная кривизна [ править ]
Многогранник можно рассматривать как поверхность с гауссовой кривизной, сосредоточенной в вершинах и определяемой угловым дефектом . Плотность многогранника равна общей кривизне (суммированной по всем его вершинам), деленной на 4π. [2]
Например, куб имеет 8 вершин, в каждой по 3 квадрата , оставляя угловой дефект π / 2. 8 × π / 2 = 4π. Итак, плотность куба равна 1.
Простые многогранники [ править ]
Плотность многогранника с простыми гранями и вершинными фигурами составляет половину характеристики Эйлера χ. Если его род является г , его плотность составляет 1 г .
- χ = V - E + F = 2 D = 2 (1- g ).
Плотность топологического многогранника сферы равна единице , как у куба .
v = 8, e = 12, f = 6.Плотность тороидального многогранника рода 1 равна нулю , как у этой гексагональной формы: v = 24, e = 48, f = 24.
Плотность тороида 5-го рода равна -4 , как этот Stewart_toroid :
v = 72, e = 168, f = 88.
Правильные звездные многогранники [ править ]
Артур Кэли использовал плотность как способ изменить формулу многогранника Эйлера ( V - E + F = 2), чтобы она работала для правильных звездных многогранников , где d v - плотность вершинной фигуры , d f - грани и D - многогранника. в целом:
- [3]
Например, большой икосаэдр {3, 5/2} имеет 20 треугольных граней ( d f = 1), 30 ребер и 12 пентаграммических вершинных фигур ( d v = 2), что дает
- 2 · 12 - 30 + 1 · 20 = 14 = 2 D .
Это означает плотность 7. Не измененная формула многогранника Эйлера не работает для малого звездчатого додекаэдра {5/2, 5} и его двойного большого додекаэдра {5, 5/2}, для которых V - E + F = −6.
Правильные звездчатые многогранники существуют в двух двойных парах, причем каждая фигура имеет ту же плотность, что и двойственная: одна пара (малый звездчатый додекаэдр - большой додекаэдр) имеет плотность 3, а другая ( большой звездчатый додекаэдр - большой икосаэдр) имеет плотность плотность 7.
| Невыпуклый большой икосаэдр {3,5 / 2} имеет плотность 7, как показано на этом прозрачном виде в разрезе справа. | |
Общие звездные многогранники [ править ]
Эдмунд Гесс обобщил формулу для звездных многогранников с разными типами граней, некоторые из которых могут складываться задом поверх других. Результирующее значение плотности соответствует тому, сколько раз связанный сферический многогранник покрывает сферу.
Это позволило Coxeter et al. для определения плотности большинства однородных многогранников , которые имеют один тип вершины и несколько типов граней. [4]
Плотность восьмиугольной призмы , обернутой дважды, составляет 2 , {8/2} × {}, показанная здесь со смещенными вершинами для ясности.
v = 16, e = 24
f 1 = 8 {4}, f 2 = 2 {8/2}
с d f1 = 1, d f2 = 2, d v = 1.Плотность пентаграммической призмы , {5/2} × {} равна 2 .
v = 10, e = 15,
f 1 = 5 {4}, f 2 = 2 {5/2},
d f1 = 1, d f2 = 2.
Неориентируемые многогранники [ править ]
Для гемиполиэдров , часть граней которых проходит через центр, плотность не может быть определена. Неориентируемые многогранники также не имеют четко определенной плотности.
Правильные 4-многогранники [ править ]
Существует 10 правильных звездных 4-многогранников (называемых 4-многогранниками Шлефли – Гесса ) с плотностями между 4, 6, 20, 66, 76 и 191. Они входят в двойственные пары, за исключением самодвойственного. Плотность-6 и плотность-66 фигур.
Заметки [ править ]
- ^ Кокстер, HS M; Красота геометрии: Двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (206-214, Плотность регулярных сот в гиперболическом пространстве)
- ^ Геометрия и воображение в Миннеаполисе 17. Угловой дефект многогранника; 20. Кривизна поверхностей; 21. Гауссова кривизна; 27.3.1 Кривизна многогранников стр. 32-51
- ^ Cromwell, P .; Многогранники , CUP hbk (1997), pbk. (1999). (Стр. 258)
- ^ Coxeter, 1954 (Раздел 6, Плотность и Таблица 7, Однородные многогранники)
Ссылки [ править ]
- Кокстер, HSM; Регулярные многогранники , (3-е издание, 1973), Дуврское издание, ISBN 0-486-61480-8
- Кокстер, HSM ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Серия А. физико - математических наук , 246 (916): 401-450, DOI : 10.1098 / rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446
- Веннингер, Магнус Дж. (1979), «Введение в понятие многогранной плотности», Сферические модели , Архив CUP, стр. 132–134 , ISBN 978-0-521-22279-2
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Плотность многоугольника» . MathWorld .