Вектор Пойнтинга

Дипольное излучение диполя вертикально на странице, показывающее напряженность электрического поля (цвет) и вектор Пойнтинга (стрелки) в плоскости страницы.

Электромагнетизм
Статьи о

Электричество Магнетизм История Учебники
Электростатика Электрический заряд Закон Кулона Дирижер Плотность заряда Разрешающая способность Электрический дипольный момент Электрическое поле Электрический потенциал Электрический поток / потенциальная энергия Электростатический разряд Закон Гаусса Индукция Изолятор Плотность поляризации Статическое электричество Трибоэлектричество
Магнитостатика Закон Ампера Закон Био – Савара Закон Гаусса для магнетизма Магнитное поле Магнитный поток Магнитный дипольный момент Магнитная проницаемость Магнитный скалярный потенциал Намагничивание Магнитодвижущая сила Магнитостатический потенциал Правило правой руки
Электродинамика Закон силы Лоренца Электромагнитная индукция Закон Фарадея Закон Ленца Ток смещения Магнитный векторный потенциал Уравнения Максвелла Электромагнитное поле Электромагнитный импульс Электромагнитное излучение Тензор Максвелла Вектор Пойнтинга Потенциал Льенара – Вихерта Уравнения Ефименко Вихревой ток Уравнения Лондона Математические описания электромагнитного поля.
Электрическая сеть Переменный ток Емкость Постоянный ток Электрический ток Электролиз Плотность тока Джоулевое нагревание Электродвижущая сила Импеданс Индуктивность Закон Ома Параллельная схема Сопротивление Резонансные полости Последовательная схема Напряжение Волноводы
Ковариантная формулировка Электромагнитный тензор ( тензор энергии-импульса ) Четырехтоковый Электромагнитный четырехпотенциальный
Ученые Ампер Биот Кулон Дэви Эйнштейн Фарадей Физо Гаусс Хевисайд Генри Герц Джоуль Ленц Лоренц Максвелл Ørsted Ом Ричи Savart Певица Тесла Вольта Вебер
v т е

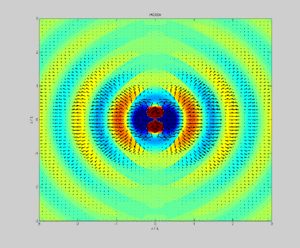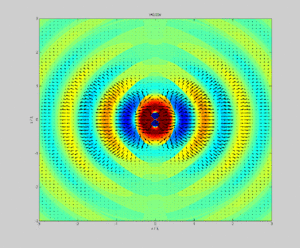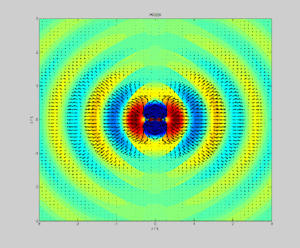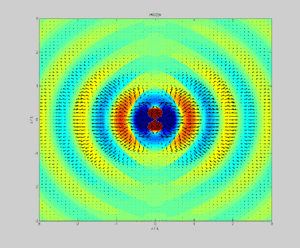
В физике , то вектор Пойнтинга представляет собой направленный поток энергии (передачу энергии на единицу площади за единицу времени) в качестве электромагнитного поля . СИ единица вектора Пойнтинга является ватт на квадратный метр (Вт / м ² ). Он назван в честь его первооткрывателя Джона Генри Пойнтинга, который первым вывел его в 1884 году. ^[1]^{: 132} Оливер Хевисайд также независимо открыл его в более общей форме, которая признает свободу добавления ротора произвольного векторного поля к определению. ^[2] Вектор Пойнтинга используется повсюдуэлектромагнетизм в сочетании с теоремой Пойнтинга , уравнением неразрывности, выражающим сохранение электромагнитной энергии , для расчета потока мощности в электрических и магнитных полях.

Определение [ править ]

В оригинальной статье Пойнтинга и во многих учебниках вектор Пойнтинга определяется как ^[3]^[4]^[5]

{\ Displaystyle \ mathbf {S} = \ mathbf {E} \ times \ mathbf {H},}

где жирные буквы обозначают векторы, а

E - вектор электрического поля ;
H - вектор вспомогательного поля магнитного поля .

Это выражение часто называют формой Авраама . ^[6] вектор Пойнтинга обычно обозначается S или N .

В «микроскопической» версии уравнений Максвелла это определение необходимо заменить определением в терминах электрического поля E и магнитного поля B (описанного далее в статье).

Также возможно объединить поле электрического смещения D с магнитным полем B, чтобы получить форму Минковского вектора Пойнтинга, или использовать D и H, чтобы построить еще одну версию. Выбор был спорным: Pfeifer et al. ^[7] суммируют и в определенной степени разрешают многовековой спор между сторонниками форм Авраама и Минковского (см. Противоречие Абрахама и Минковского ).

Вектор Пойнтинга представляет собой частный случай вектора потока энергии для электромагнитной энергии. Однако любой тип энергии имеет свое направление движения в пространстве, а также свою плотность, поэтому векторы потока энергии могут быть определены и для других типов энергии, например, для механической энергии . Вектор Умова – Пойнтинга ^[8], открытый Николаем Умовым в 1874 году, описывает поток энергии в жидких и упругих средах в полностью обобщенном виде.

Интерпретация [ править ]

Цепь постоянного тока, состоящая из батареи ( V ) и резистора ( R ), показывающая направление вектора Пойнтинга ( S , синие стрелки ) в окружающем его пространстве, а также поля, из которых он получен; электрическое поле ( Е , красные стрелки ) и магнитное поле ( Н , зеленые стрелки ). В области вокруг батареи вектор Пойнтинга направлен наружу, указывая на то, что мощность, вытекающая из батареи в поля; в области вокруг резистора вектор направлен внутрь, указывая на мощность поля, протекающую в резистор. Через любую плоскость PМежду батареей и резистором поток Пойнтинга направлен в сторону резистора. Величины (длины) векторов не показаны точно; только направления имеют значение.

Вектор Пойнтинга фигурирует в теореме Пойнтинга (вывод см. В этой статье), законе сохранения энергии:

{\frac {\partial u}{\partial t}}=-\mathbf {\nabla } \cdot \mathbf {S} -\mathbf {J_{\mathrm {f} }} \cdot \mathbf {E} ,

где J _F представляет собой плотность тока из свободных зарядов и у является плотность электромагнитной энергии для линейных, недиспергирующих материалов, дается

u={\frac {1}{2}}\!\left(\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} \right)\!,

где

E - электрическое поле;
D - поле электрического смещения;
B - магнитное поле;
H - дополнительное магнитное поле. ^[9]^{: 258–260}

Первый член в правой части представляет поток электромагнитной энергии в небольшой объем, а второй член вычитает работу, совершаемую полем над свободными электрическими токами, которые, таким образом, выходят из электромагнитной энергии в виде рассеяния , тепла и т. Д. По определению, связанные электрические токи не включены в этот термин, а вместо этого вносят вклад в S и u .

Для линейных, недисперсных и изотропных (для простоты) материалов определяющие соотношения можно записать в виде

\mathbf {D} =\varepsilon \mathbf {E} ,\quad \mathbf {H} ={\frac {1}{\mu }}\mathbf {B} ,

где

ε - диэлектрическая проницаемость материала;
μ - проницаемость материала. ^[9]^{: 258–260}

Здесь ε и μ - скалярные действительные константы, не зависящие от положения, направления и частоты.

В принципе, это ограничивает теорему Пойнтинга в такой форме полями в вакууме и недисперсными линейными материалами. Обобщение на дисперсные материалы возможно при определенных обстоятельствах за счет дополнительных условий. ^[9]^{: 262–264}

Одним из следствий формулы Пойнтинга является то, что для того, чтобы электромагнитное поле работало, должны присутствовать как магнитное, так и электрическое поля. Одно только магнитное поле и одно электрическое поле не могут сделать никакой работы. ^[10]

Формулировка в терминах микроскопических полей [ править ]

«Микроскопическая» (дифференциальная) версия уравнений Максвелла допускает только фундаментальные поля E и B , без встроенной модели материальных сред. Используются только диэлектрическая проницаемость и магнитная проницаемость вакуума, D или H отсутствуют . При использовании этой модели вектор Пойнтинга определяется как

\mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} ,

где

μ ₀ - вакуумная проницаемость ;
E - вектор электрического поля;
B - вектор магнитного поля.

Фактически это общее выражение вектора Пойнтинга. ^[11] Соответствующая форма теоремы Пойнтинга такова:

{\frac {\partial u}{\partial t}}=-\nabla \cdot \mathbf {S} -\mathbf {J} \cdot \mathbf {E} ,

где J - полная плотность тока, а плотность энергии u определяется выражением

u={\frac {1}{2}}\!\left(\varepsilon _{0}\mathbf {E} ^{2}+{\frac {1}{\mu _{0}}}\mathbf {B} ^{2}\right)\!,

где ε ₀ является вакуумной диэлектрической проницаемостью , а обозначение Е ² понимаются скалярное произведение реального вектора Е (т) с самими собой, таким образом, квадратом из векторной нормы || E ||. Его можно вывести непосредственно из уравнений Максвелла только в терминах полного заряда и тока и закона силы Лоренца .

Эти два альтернативных определение Пойнтинга вектора равно в вакууме или в немагнитных материалах, где B = ц ₀H . Во всех остальных случаях они отличаются тем, что S = (1 / μ ₀ ) E × B, а соответствующие u являются чисто радиационными, поскольку диссипативный член - J ⋅ E покрывает полный ток, а определение E × H имеет вклады от связанные токи, которые затем исключаются из диссипативного члена. ^[12]

Поскольку при выводе S = (1 / μ ₀ ) E × B и плотности энергии возникают только микроскопические поля E и B , предположения о любом присутствующем материале избегаются. Вектор Пойнтинга, теорема и выражение для плотности энергии универсально применимы для вакуума и любых материалов. ^[12]

Усредненный по времени вектор Пойнтинга [ править ]

Силовые линии усредненного по времени вектора Пойнтинга электрического диполя вблизи зеркала создают сложные картины.

Вышеупомянутая форма для вектора Пойнтинга представляет мгновенный поток энергии из-за мгновенных электрических и магнитных полей. Чаще всего проблемы в электромагнетизме решаются с помощью синусоидально изменяющихся полей на заданной частоте. Затем результаты можно применять в более общем плане, например, представляя некогерентное излучение как суперпозицию таких волн на разных частотах и с флуктуирующими амплитудами.

Таким образом, мы не будем рассматривать мгновенные $E (t)$ и $H (t),$ использованные выше, а скорее комплексную (векторную) амплитуду для каждого, которая описывает фазу когерентной волны (а также амплитуду) с использованием векторной записи. Эти комплексные векторы амплитуды не являются функциями времени, поскольку они понимаются как относящиеся к колебаниям за все время. Под вектором, например $E m$ , понимается синусоидально изменяющееся поле, мгновенная амплитуда которого $E (t)$ соответствует действительной части $E m e jωt,$ где $ω$ - частота (радиан) рассматриваемой синусоидальной волны.

Во временной области будет видно, что мгновенный поток мощности будет колебаться с частотой 2 ω . Но обычно представляет интерес средний поток мощности, в котором эти колебания не учитываются. В приведенной ниже математике это достигается интегрированием за полный цикл $T = 2 π / ω$ . Следующая величина, по-прежнему называемая «вектором Пойнтинга», выражается непосредственно через векторы как:

\mathbf {S} _{\mathrm {m} }={\tfrac {1}{2}}\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }^{*},

где ^∗ обозначает комплексное сопряжение. Поток мощности усредненных по времени ( в соответствии с мгновенным вектором Пойнтинга , усредненным по полному циклу, например) , затем задаются вещественной частью из $S м$ . Мнимая часть обычно игнорируется, однако она означает «реактивную мощность», такую как помехи из-за стоячей волны или ближнего поля антенны. В одной плоской электромагнитной волне (а не в стоячей волне, которую можно описать как две такие волны, распространяющиеся в противоположных направлениях), $E$ и $H$ точно совпадают по фазе, поэтому $S m$ - это просто действительное число в соответствии с приведенным выше определением.

Эквивалентность $Re (S m)$ среднему по времени мгновенного вектора Пойнтинга $S$ можно показать следующим образом.

{\begin{aligned}\mathbf {S} (t)&=\mathbf {E} (t)\times \mathbf {H} (t)\\&=\operatorname {Re} \!\left(\mathbf {E} _{\mathrm {m} }e^{j\omega t}\right)\times \operatorname {Re} \!\left(\mathbf {H} _{\mathrm {m} }e^{j\omega t}\right)\\&={\tfrac {1}{2}}\!\left(\mathbf {E} _{\mathrm {m} }e^{j\omega t}+\mathbf {E} _{\mathrm {m} }^{*}e^{-j\omega t}\right)\times {\tfrac {1}{2}}\!\left(\mathbf {H} _{\mathrm {m} }e^{j\omega t}+\mathbf {H} _{\mathrm {m} }^{*}e^{-j\omega t}\right)\\&={\tfrac {1}{4}}\!\left(\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }^{*}+\mathbf {E} _{\mathrm {m} }^{*}\times \mathbf {H} _{\mathrm {m} }+\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }e^{2j\omega t}+\mathbf {E} _{\mathrm {m} }^{*}\times \mathbf {H} _{\mathrm {m} }^{*}e^{-2j\omega t}\right)\\&={\tfrac {1}{2}}\operatorname {Re} \!\left(\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }^{*}\right)+{\tfrac {1}{2}}\operatorname {Re} \!\left(\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }e^{2j\omega t}\right)\!.\end{aligned}}

Среднее значение мгновенного вектора Пойнтинга S с течением времени определяется как:

\langle \mathbf {S} \rangle ={\frac {1}{T}}\int _{0}^{T}\mathbf {S} (t)\,dt={\frac {1}{T}}\int _{0}^{T}\!\left[{\tfrac {1}{2}}\operatorname {Re} \!\left(\mathbf {E} _{\mathrm {m} }\times \mathbf {H} _{\mathrm {m} }^{*}\right)+{\tfrac {1}{2}}\operatorname {Re} \!\left({\mathbf {E} _{\mathrm {m} }}\times {\mathbf {H} _{\mathrm {m} }}e^{2j\omega t}\right)\right]dt.

Второй член - это двухчастотная составляющая, имеющая среднее значение, равное нулю, поэтому мы находим:

\langle \mathbf {S} \rangle =\operatorname {Re} \!\left({\tfrac {1}{2}}{\mathbf {E} _{\mathrm {m} }}\times \mathbf {H} _{\mathrm {m} }^{*}\right)=\operatorname {Re} \!\left(\mathbf {S} _{\mathrm {m} }\right)

Согласно некоторым соглашениям коэффициент 1/2 в приведенном выше определении может быть опущен. Умножение на 1/2 требуется для правильного описания потока мощности, поскольку величины $E m$ и $H m$ относятся к пиковым полям осциллирующих величин. Если, скорее, поля описываются в терминах их среднеквадратичных (среднеквадратичных) значений (каждое из которых меньше на коэффициент ), то правильный средний поток мощности получается без умножения на 1/2. ${\sqrt {2}}/2$

Примеры и приложения [ править ]

Коаксиальный кабель [ править ]

Вектор Пойнтинга в коаксиальном кабеле, показан красным.

Например, вектор Пойнтинга внутри диэлектрического изолятора в виде коаксиального кабеля почти параллельно оси проволоки (не предполагая полей снаружи кабеля и длиной волны длиннее , чем диаметр кабеля, в том числе DC). Электрическая энергия, подаваемая на нагрузку, полностью проходит через диэлектрик между проводниками . В самих проводниках течет очень мало энергии, так как напряженность электрического поля почти равна нулю. Энергия, протекающая в проводниках, течет в проводники радиально и учитывает потерю энергии на резистивный нагрев проводника. За пределами кабеля энергия также не течет, поскольку там магнитные поля внутренних и внешних проводников сводятся к нулю.

Резистивное рассеивание [ править ]

Если проводник имеет значительное сопротивление, то вблизи поверхности этого проводника вектор Пойнтинга будет наклонен к проводнику и столкнется с ним. Как только вектор Пойнтинга входит в проводник, он изгибается в направлении, почти перпендикулярном поверхности. ^[13]^{: 61} Это следствие закона Снеллиуса и очень медленной скорости света внутри проводника. Можно дать определение и вычисление скорости света в проводнике. ^[14]^{: 402} Внутри проводника вектор Пойнтинга представляет собой поток энергии из электромагнитного поля в провод, вызывая резистивный джоулев нагрев.в проводе. Для вывода, который начинается с закона Снеллиуса, см. Reitz, стр. 454. ^[15]^{: 454}

Плоские волны [ править ]

В распространяющейся синусоидальной линейно поляризованной электромагнитной плоской волне с фиксированной частотой вектор Пойнтинга всегда указывает в направлении распространения, колеблясь по величине. Усредненная по времени величина вектора Пойнтинга находится, как указано выше, равной:

\langle S\rangle ={\frac {1}{2\eta }}|E_{\mathrm {m} }|^{2}

где E _m - комплексная амплитуда электрического поля, а η - характеристический импеданс передающей среды, или просто $η 0$ ≈ 377 Ом для плоской волны в свободном пространстве. Это непосредственно следует из приведенного выше выражения для среднего вектора Пойнтинга с использованием векторных величин и того факта, что в плоской волне магнитное поле $H m$ равно электрическому полю $E m,$ деленному на η (и, следовательно, точно по фазе).

В оптике усредненное по времени значение излучаемого потока технически известно как энергетическая освещенность , чаще просто интенсивность .

Радиационное давление [ править ]

Плотность импульса электромагнитного поля равна S / c ^2, где S - величина вектора Пойнтинга, а c - скорость света в свободном пространстве. Давление излучения , оказываемое электромагнитной волны на поверхности мишени задается

P_{\mathrm {rad} }={\frac {\langle S\rangle }{\mathrm {c} }}.

Статические поля [ править ]

Вектор Пойнтинга в статическом поле, где E - электрическое поле, H - магнитное поле, а S - вектор Пойнтинга.

Рассмотрение вектора Пойнтинга в статических полях показывает релятивистский характер уравнений Максвелла и позволяет лучше понять магнитную составляющую силы Лоренца , q ( v × B ) . Для иллюстрации рассмотрено сопроводительное изображение, которое описывает вектор Пойнтинга в цилиндрическом конденсаторе, который находится в поле H (указывает на страницу), создаваемом постоянным магнитом. Хотя существуют только статические электрические и магнитные поля, вычисление вектора Пойнтинга создает круговой поток электромагнитной энергии по часовой стрелке без начала и конца.

Хотя циркулирующий поток энергии может показаться нелогичным, необходимо поддерживать сохранение углового момента . Плотность импульса пропорциональна плотности потока энергии, поэтому циркулирующий поток энергии содержит угловой момент. ^[16] Это причина магнитной составляющей силы Лоренца, которая возникает, когда конденсатор разряжен. Во время разряда угловой момент, содержащийся в потоке энергии, истощается, поскольку он передается зарядам разрядного тока, пересекающим магнитное поле.

Добавление завитка векторного поля [ править ]

Вектор Пойнтинга встречается в теореме Пойнтинга только через его расходимость ∇ ⋅ S , то есть требуется только, чтобы поверхностный интеграл вектора Пойнтинга вокруг замкнутой поверхности описывал чистый поток электромагнитной энергии в замкнутый объем или из него. Это означает, что добавление соленоидального векторного поля (одно с нулевой дивергенцией) к S приведет к другому полю, которое удовлетворяет этому требуемому свойству векторного поля Пойнтинга согласно теореме Пойнтинга. Поскольку дивергенция любого ротора равна нулю , можно добавить ротор любого векторного поля к вектору Пойнтинга и полученному векторному полю S 'по-прежнему удовлетворяет теореме Пойнтинга. ^[9]^{: 258–260}

Однако специальная теория относительности , в которой энергия и импульс определяются локально и инвариантно с помощью тензора энергии-импульса , показывает, что данное выше выражение для вектора Пойнтинга единственно. ^[9]^{: 258–260 605–612}

Ссылки [ править ]

^ Страттон, Джулиус Адамс (1941). Электромагнитная теория (1-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-470-13153-4.
^ Nahin, Paul J. (2002). Оливер Хевисайд: жизнь, работа и времена гения-электрика викторианской эпохи . п. 131. ISBN. 9780801869099.
^ Пойнтинг, Джон Генри (1884). «О передаче энергии в электромагнитном поле» . Философские труды Лондонского королевского общества . 175 : 343–361. DOI : 10,1098 / rstl.1884.0016 .
^ Грант, Ян С .; Филлипс, Уильям Р. (1990). Электромагнетизм (2-е изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-92712-9.
^ Гриффитс, Дэвид Дж. (2012). Введение в электродинамику (3-е изд.). Бостон: Эддисон-Уэсли. ISBN 978-0-321-85656-2.
^ Кинслер, Пол; Фаваро, Альберто; Макколл, Мартин В. (2009). «Четыре теоремы Пойнтинга». Европейский журнал физики . 30 (5): 983. arXiv : 0908.1721 . Bibcode : 2009EJPh ... 30..983K . DOI : 10.1088 / 0143-0807 / 30/5/007 .
^ Пфайфер, Роберт NC; Nieminen, Timo A .; Heckenberg, Norman R .; Рубинштейн-Данлоп, Галина (2007). «Импульс электромагнитной волны в диэлектрических средах». Обзоры современной физики . 79 (4): 1197. arXiv : 0710.0461 . Bibcode : 2007RvMP ... 79.1197P . DOI : 10.1103 / RevModPhys.79.1197 .
^ Умов, Николай Алексеевич (1874). «Теорема Ein über die Wechselwirkungen в Endlichen Entfernungen» . Zeitschrift für Mathematik und Physik . 19 : 97–114.
^ a b c d e Джексон, Джон Дэвид (1998). Классическая электродинамика (3-е изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-30932-1.
^ "Примеры физики К. Макдональда - Рейлган" (PDF) . puhep1.princeton.edu . Источник 2021-02-14 .
^ Зангвилл, Эндрю (2013). Современная электродинамика . Издательство Кембриджского университета. п. 508. ISBN 9780521896979.
^ a b Рихтер, Феликс; Флориан, Матиас; Хеннебергер, Клаус (2008). «Теорема Пойнтинга и сохранение энергии при распространении света в ограниченных средах». EPL . 81 (6): 67005. arXiv : 0710.0515 . Bibcode : 2008EL ..... 8167005R . DOI : 10.1209 / 0295-5075 / 81/67005 .
^ Харрингтон, Роджер Ф. (2001). Гармонические во времени электромагнитные поля (2-е изд.). Макгроу-Хилл. ISBN 978-0-471-20806-8.
^ Хейт, Уильям (2011). Инженерная электромагнетизм (4-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-07-338066-7.
^ Reitz, Джон R .; Милфорд, Фредерик Дж .; Кристи, Роберт В. (2008). Основы электромагнитной теории (4-е изд.). Бостон: Эддисон-Уэсли. ISBN 978-0-321-58174-7.
^ Фейнман, Ричард Филлипс (2011). Лекции Фейнмана по физике . Vol. II: В основном электромагнетизм и материя (изд. Новое тысячелетие). Нью-Йорк: Основные книги. ISBN 978-0-465-02494-0.

Дальнейшее чтение [ править ]

В Викицитатнике есть цитаты, связанные с: вектором Пойнтинга

В Викиверситете есть урок по теореме Пойнтинга

Беккер, Ричард (1982). Электромагнитные поля и взаимодействия (1-е изд.). Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-64290-1.
Эдминистер, Джозеф; Нахви, Махмуд (2013). Электромагнетизм (4-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-07-183149-9.

[Stratton1941-1] Страттон, Джулиус Адамс (1941). Электромагнитная теория (1-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-470-13153-4.

[Nahin2002-2] Nahin, Paul J. (2002). Оливер Хевисайд: жизнь, работа и времена гения-электрика викторианской эпохи . п. 131. ISBN. 9780801869099.

[Poynting1884-3] Пойнтинг, Джон Генри (1884). «О передаче энергии в электромагнитном поле» . Философские труды Лондонского королевского общества . 175 : 343–361. DOI : 10,1098 / rstl.1884.0016 .

[4] Грант, Ян С .; Филлипс, Уильям Р. (1990). Электромагнетизм (2-е изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-92712-9.

[5] Гриффитс, Дэвид Дж. (2012). Введение в электродинамику (3-е изд.). Бостон: Эддисон-Уэсли. ISBN 978-0-321-85656-2.

[Kinsler2009-6] Кинслер, Пол; Фаваро, Альберто; Макколл, Мартин В. (2009). «Четыре теоремы Пойнтинга». Европейский журнал физики . 30 (5): 983. arXiv : 0908.1721 . Bibcode : 2009EJPh ... 30..983K . DOI : 10.1088 / 0143-0807 / 30/5/007 .

[Pfeifer2007-7] Пфайфер, Роберт NC; Nieminen, Timo A .; Heckenberg, Norman R .; Рубинштейн-Данлоп, Галина (2007). «Импульс электромагнитной волны в диэлектрических средах». Обзоры современной физики . 79 (4): 1197. arXiv : 0710.0461 . Bibcode : 2007RvMP ... 79.1197P . DOI : 10.1103 / RevModPhys.79.1197 .

[Umov1874-8] Умов, Николай Алексеевич (1874). «Теорема Ein über die Wechselwirkungen в Endlichen Entfernungen» . Zeitschrift für Mathematik und Physik . 19 : 97–114.

[Jackson1998-9] Джексон, Джон Дэвид (1998). Классическая электродинамика (3-е изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-30932-1.

[10] "Примеры физики К. Макдональда - Рейлган" (PDF) . puhep1.princeton.edu . Источник 2021-02-14 .

[11] Зангвилл, Эндрю (2013). Современная электродинамика . Издательство Кембриджского университета. п. 508. ISBN 9780521896979.

[Richter2008-12] Рихтер, Феликс; Флориан, Матиас; Хеннебергер, Клаус (2008). «Теорема Пойнтинга и сохранение энергии при распространении света в ограниченных средах». EPL . 81 (6): 67005. arXiv : 0710.0515 . Bibcode : 2008EL ..... 8167005R . DOI : 10.1209 / 0295-5075 / 81/67005 .

[Harrington2001-13] Харрингтон, Роджер Ф. (2001). Гармонические во времени электромагнитные поля (2-е изд.). Макгроу-Хилл. ISBN 978-0-471-20806-8.

[Hayt2011-14] Хейт, Уильям (2011). Инженерная электромагнетизм (4-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-07-338066-7.

[Reitz2008-15] Reitz, Джон R .; Милфорд, Фредерик Дж .; Кристи, Роберт В. (2008). Основы электромагнитной теории (4-е изд.). Бостон: Эддисон-Уэсли. ISBN 978-0-321-58174-7.

[Feynman-16] Фейнман, Ричард Филлипс (2011). Лекции Фейнмана по физике . Vol. II: В основном электромагнетизм и материя (изд. Новое тысячелетие). Нью-Йорк: Основные книги. ISBN 978-0-465-02494-0.