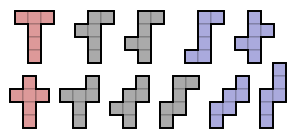Гексамин (или 6-omino ) является Полимином порядка 6, то есть многоугольник в плоскости выполнен из 6 равных по размеру квадратов , соединенных от края до края. [1] Название этого типа фигур состоит из префикса hex (a) - . Когда вращения и отражения не считаются отдельными формами, существует 35 различных свободных гексомино. Когда отражения считаются отчетливыми, получается 60 односторонних гексомино. Когда повороты также считаются отдельными, существует 216 фиксированныхгексомино. [2] [3]
Симметрия [ править ]
На рисунке выше показаны все 35 возможных свободных гексомино, раскрашенных в соответствии с их группами симметрии :
- Двадцать серых гексомино не имеют симметрии . Их группа симметрии состоит только из тождественного отображения .
- Шесть красных гексомино имеют ось зеркальной симметрии, параллельную линиям сетки. Их группа симметрии состоит из двух элементов: идентичности и отражения на линии, параллельной сторонам квадратов.
- Два зеленых гексомино имеют ось зеркальной симметрии под углом 45 ° к линиям сетки. Их группа симметрии состоит из двух элементов: тождества и диагонального отражения.
- Пять синих гексомино обладают точечной симметрией, также известной как вращательная симметрия второго порядка. Их группа симметрии состоит из двух элементов: идентичности и поворота на 180 °.
- Два фиолетовых гексомино имеют две оси зеркальной симметрии, обе параллельны линиям сетки (таким образом, одна горизонтальная ось и одна вертикальная ось). Их группа симметрии состоит из четырех элементов. Это диэдральная группа порядка 2, также известная как четырехгруппа Клейна .
Если отражения гексомино считаются отдельными, как в случае односторонних гексомино, то каждая из указанных выше категорий первой и четвертой будет вдвое больше, что приведет к дополнительным 25 гексомино, всего 60. Если вращения также считаются отдельными, тогда гексомино из первой категории засчитываются восьмикратно, из следующих трех категорий засчитываются четырехкратно, а из последней категории засчитываются дважды. В результате получается 20 × 8 + (6 + 2 + 5) × 4 + 2 × 2 = 216 фиксированных гексомино.
Упаковка и укладка [ править ]
Каждое из 35 гексомино удовлетворяет критерию Конвея ; следовательно, каждое гексомино способно разбить плоскость. [4]
Хотя полный набор из 35 гексомино состоит из 210 квадратов, уложить их в прямоугольник невозможно . (Такое расположение возможно с 12 пентамино, которые могут быть упакованы в любой из прямоугольников 3 × 20, 4 × 15, 5 × 12 и 6 × 10). Простой способ продемонстрировать, что такая упаковка гексомино невозможна. через аргумент четности . Если гексомино расположены в шахматном порядке, то 11 гексомино будут покрывать четное количество черных квадратов (либо 2 белых и 4 черных, либо наоборот), а остальные 24 гексомино будут покрывать нечетное число.черных квадратов (3 белых и 3 черных). В целом, при любом расположении будет покрыто четное количество черных квадратов. Однако любой прямоугольник из 210 квадратов будет иметь 105 черных квадратов и 105 белых квадратов, и поэтому не может быть покрыт 35 гексомино.
Однако есть и другие простые фигуры из 210 квадратов, которые можно заполнить гексомино. Например, квадрат 15 × 15 с удаленным из центра прямоугольником 3 × 5 имеет 210 квадратов. При расцветке шахматной доски он имеет 106 белых и 104 черных квадрата (или наоборот), поэтому паритет не препятствует упаковке, и упаковка действительно возможна. [5] Также возможно, чтобы два набора фигур соответствовали прямоугольнику размера 420 или для набора из 60 односторонних гексомино (18 из которых покрывают четное количество черных квадратов), чтобы поместиться в прямоугольник размера 360. [6]
Многогранные сети для куба [ править ]
Многогранная сетка для куба обязательно является гексаминой, с 11 гексомиными (показано справа) фактически сетями. Они появляются справа, снова окрашенные в соответствии с их группами симметрии.
Полиэдрическая сетка для куба не может содержать ни О-тетромино, ни I-пентамино, U-пентамино или V-пентамино.
Ссылки [ править ]
- ^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8.
- ^ Вайсштейн, Эрик В. "Гексомино" . Материал из MathWorld - веб-ресурса Wolfram . Проверено 22 июля 2008 .
- ^ Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика . 36 : 191–203. DOI : 10.1016 / 0012-365X (81) 90237-5 .
- Перейти ↑ Rhoads, Glenn C. (2003). Плоские мозаики и поиск апериодического прототила . Кандидатская диссертация, Университет Рутгерса.
- ^ Mathematische Basteleien: Hexominos (на английском языке)
- ^ Конструкции Hexomino
Внешние ссылки [ править ]
- Страница Юргена Кёллера о гексомино, включая симметрию, упаковку и другие аспекты
- Полимин страница из David Эпштайна «s Геометрия Junkyard
- Одиннадцать анимаций, показывающих узоры куба (на французском языке)
- Полиполигональные мозаики , Стивен Датч.