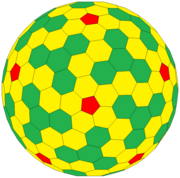
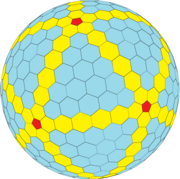
В математике , а точнее в полиэдральной комбинаторике , многогранник Гольдберга - это выпуклый многогранник, состоящий из шестиугольников и пятиугольников. Впервые они были описаны Майклом Голдбергом (1902–1990) в 1937 году. Они определяются тремя свойствами: каждая грань представляет собой пятиугольник или шестиугольник, ровно три грани пересекаются в каждой вершине, и они обладают вращательной икосаэдрической симметрией . Они не обязательно зеркально-симметричны; например, GP (5,3) и GP (3,5) являются энантиоморфами друг друга. Голдберг многогранник представляет собой двойной многогранник из геодезической сферы .
Следствием формулы многогранника Эйлера является то, что многогранник Гольдберга всегда имеет ровно двенадцать пятиугольных граней. Икосаэдрическая симметрия гарантирует, что пятиугольники всегда правильны и их всегда 12. Если вершины не ограничены сферой, многогранник может быть построен с плоскими равносторонними (но не в общем случае равносторонними) гранями.
Простые примеры многогранников Гольдберга включают додекаэдр и усеченный икосаэдр . Другие формы можно описать ходом шахматного коня от одного пятиугольника к другому: сначала сделайте m шагов в одном направлении, затем поверните на 60 ° влево и сделайте n шагов. Такой многогранник обозначается GP ( m , n ). Додекаэдр - это GP (1,0), а усеченный икосаэдр - это GP (1,1).
Похожая техника может быть применена для построения многогранников с тетраэдрической симметрией и октаэдрической симметрией . Эти многогранники будут иметь треугольники или квадраты, а не пятиугольники. Этим вариациям даны индексы римских цифр, обозначающие количество сторон на гранях, отличных от шестиугольника: GP III (n, m), GP IV (n, m) и GP V (n, m).
Элементы [ править ]
Количество вершин, ребер и граней GP ( m , n ) может быть вычислено из m и n , с T = m 2 + mn + n 2 = ( m + n ) 2 - mn , в зависимости от одной из трех симметрий. системы: [1] Количество негексагональных граней можно определить с помощью характеристики Эйлера, как показано здесь .
| Симметрия | Икосаэдр | Восьмигранный | Тетраэдр |
|---|---|---|---|
| Основание | Додекаэдр GP V (1,0) = {5 +, 3} 1,0 | Куб GP IV (1,0) = {4 +, 3} 1,0 | Тетраэдр GP III (1,0) = {3 +, 3} 1,0 |
| Изображение |  |  |  |
| Символ | GP V (m, n) = {5 +, 3} m, n | GP IV (m, n) = {4 +, 3} m, n | GP III (m, n) = {3 +, 3} m, n |
| Вершины | |||
| Края | |||
| Лица | |||
| Лица по типу | 12 {5} и 10 ( Т - 1) {6} | 6 {4} и 4 ( Т - 1) {6} | 4 {3} и 2 ( Т - 1) {6} |
Строительство [ править ]
Большинство многогранников Гольдберга могут быть построены с использованием нотации многогранников Конвея, начиная с (T) этраэдра, (C) ube и (D) семян одекаэдра. Фаска оператор, с , заменяет все ребра шестиугольников, превращая ГП ( м , п ) к ГПУ (2 м , 2 л ), с T множителем 4. усечены кис оператором, у = ки , порождает GP (3, 0), преобразуя GP ( m , n ) в GP (3 m , 3n ) с множителем T равным 9.
Для форм класса 2 двойственный оператор kis , z = dk , преобразует GP ( a , 0) в GP ( a , a ) с множителем T, равным 3. Для форм класса 3 оператор вихря , w , генерирует GP ( 2,1), с множителем T, равным 7. Генератор вихрей по часовой стрелке и против часовой стрелки, w w = wrw генерирует GP (7,0) в классе 1. В общем, вихрь может преобразовать GP ( a , b ) в GP. ( а + 3 b , 2 ab ) для a > b и того же кирального направления. Если киральные направления меняются местами, GP ( a , b ) становится GP (2 a + 3 b , a - 2 b ), если a ≥ 2 b , и GP (3 a + b , 2 b - a ), если a <2 b .
Примеры [ править ]
| Частота | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) | (8,0) | ( м , 0) |
|---|---|---|---|---|---|---|---|---|---|
| Т | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | м 2 |
| Икосаэдр (Гольдберг) | правильный додекаэдр | додекаэдр с фаской | более | ||||||
| Восьмигранный | куб | куб с фаской | более | ||||||
| Тетраэдр | тетраэдр | тетраэдр с фаской | более |
| Частота | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | ( м , м ) |
|---|---|---|---|---|---|---|---|---|---|
| Т | 3 | 12 | 27 | 48 | 75 | 108 | 147 | 192 | 3 м 2 |
| Икосаэдр (Гольдберг) | усеченный икосаэдр | более | |||||||
| Восьмигранный | усеченный октаэдр | более | |||||||
| Тетраэдр | усеченный тетраэдр | более |
| Частота | (1,2) | (1,3) | (2,3) | (1,4) | (2,4) | (3,4) | (1,5) | ( м , п ) |
|---|---|---|---|---|---|---|---|---|
| Т | 7 | 13 | 19 | 21 год | 28 год | 37 | 31 год | м 2 + мн + п 2 |
| Икосаэдр (Гольдберг) | более | |||||||
| Восьмигранный | более | |||||||
| Тетраэдр | более |
См. Также [ править ]
- Капсид
- Геодезическая сфера
- Фуллерен # Другие бакиболлы
- Обозначения многогранника Конвея
- Построение Гольдберга – Кокстера.
Заметки [ править ]
- ^ Гипотеза Клинтона о равном центральном угле, ДЖОЗЕФ Д. КЛИНТОН
Ссылки [ править ]
- Гольдберг, Майкл (1937). «Класс мультисимметричных многогранников» . Математический журнал Тохоку .
- Джозеф Д. Клинтон, гипотеза Клинтона о равных центральных углах
- Харт, Джордж (2012). «Многогранники Гольдберга». В Сенешале, Марджори (ред.). Формируя пространство (2-е изд.). Springer. С. 125–138. DOI : 10.1007 / 978-0-387-92714-5_9 . [1]
- Харт, Джордж (18 июня 2013 г.). «Математические впечатления: многогранники Гольдберга» . Саймонс Новости науки.
- Schein, S .; Гейед, Дж. М. (25 февраля 2014 г.). «Четвертый класс выпуклых равносторонних многогранников с многогранной симметрией, относящийся к фуллеренам и вирусам» . Труды Национальной академии наук . 111 (8): 2920–2925. DOI : 10.1073 / pnas.1310939111 . ISSN 0027-8424 . PMC 3939887 . PMID 24516137 .
Внешние ссылки [ править ]
- Двойные геодезические икосаэдры
- Варианты Гольдберга: новые формы для молекулярных каркасов Плоские шестиугольники и пятиугольники объединяются в новом повороте старого многогранника, Дана Маккензи, 14 февраля 2014 г.