| Усеченный икосододекаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Однородный многогранник |
| Элементы | F = 62, E = 180, V = 120 (χ = 2) |
| Лица по сторонам | 30 {4} +20 {6} +12 {10} |
| Обозначение Конвея | bD или taD |
| Символы Шлефли | tr {5,3} или |
| т 0,1,2 {5,3} | |
| Символ Wythoff | 2 3 5 | |
| Диаграмма Кокстера | |
| Группа симметрии | I h , H 3 , [5,3], (* 532), заказ 120 |
| Группа вращения | I , [5,3] + , (532), порядок 60 |
| Двугранный угол | 6-10: 142,62 ° 4-10: 148,28 ° 4-6: 159,095 ° |
| Рекомендации | U 28 , C 31 , W 16 |
| Характеристики | Полуправильный выпуклый зоноэдр |
 Цветные лица |  4.6.10 ( Вершина ) |
 Триаконтаэдр Дисдякиса ( двойственный многогранник ) | 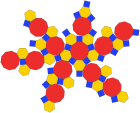 Сеть |
В геометрии , то усеченная икосододекаэдр является архимедовой твердым веществом , один из тринадцати выпуклых изогонального nonprismatic твердых веществ , построенных двух или более типов правильных многоугольника граней .
У него 62 грани: 30 квадратов , 20 правильных шестиугольников и 12 правильных десятиугольников . У него больше всего ребер и вершин среди всех Платоновых и Архимедовых тел, хотя у курносого додекаэдра больше граней. Из всех вершинно-транзитивных многогранников он занимает наибольший процент (89,80%) от объема сферы, в которую он вписан, очень узко опережая курносый додекаэдр (89,63%) и Малый ромбикосододекаэдр (89,23%), и менее узко опережая его. Усеченный икосаэдр(86,74%); он также имеет наибольший объем (206,8 кубических единиц), когда длина его ребра равна 1. Из всех вершинно-транзитивных многогранников, не являющихся призмами или антипризмами, он имеет наибольшую сумму углов (90 + 120 + 144 = 354 градуса). в каждой вершине; только призма или антипризма с более чем 60 сторонами будет иметь большую сумму. Так как каждый из его граней имеет точечную симметрию ( что эквивалентно, 180 ° вращения симметрии), усеченный икосододекаэдр является зоноэдром .
Имена [ править ]
Название усеченный икосододекаэдр , данное первоначально Иоганном Кеплером , вводит в заблуждение. Фактическое усечение из икосододекаэдр имеет прямоугольники вместо квадратов . Этот неоднородный многогранник топологически эквивалентен архимедову твердому телу. Альтернативные взаимозаменяемые имена:
| Икосидодекаэдр и его усечение |
Название большой ромбикосододекаэдр относится к родству с (малым) ромбикосододекаэдром (сравните раздел Диссекция ).
Существует невыпуклый однородный многогранник с похожим названием невыпуклый большой ромбикосододекаэдр .
Площадь и объем [ править ]
Площадь поверхности A и объем V усеченного икосододекаэдра с длиной ребра a равны: [ необходима цитата ]
Если бы набор всех 13 архимедовых тел был построен с равной длиной ребер, усеченный икосододекаэдр был бы самым большим.
Декартовы координаты [ править ]
Декартовы координаты вершин усеченного икосододекаэдра с длиной ребра 2 φ - 2 с центром в начале координат представляют собой все четные перестановки : [4]
- (±1/φ, ±1/φ, ± (3 + φ )),
- (±2/φ, ± φ , ± (1 + 2 φ )),
- (±1/φ, ± φ 2 , ± (−1 + 3 φ )),
- (± (2 φ - 1), ± 2, ± (2 + φ )) и
- (± φ , ± 3, ± 2 φ ),
где φ = 1 + √ 5/2это золотое сечение .
Рассечение [ править ]
Усечен икосододекаэдром является выпуклой оболочкой из ромбоикосододекаэдра с кубоидами выше его 30 квадратов, у которых отношение высоты к базовому является φ . Остальное пространство можно разделить на неоднородные купола, а именно 12 между внутренними пятиугольниками и внешними декагонами и 20 между внутренними треугольниками и внешними шестиугольниками .
Альтернативное рассечение также имеет ромбикосододекаэдрическое ядро. Он имеет 12 пятиугольных ротондов между внутренними пятиугольниками и внешними декагонами. Оставшаяся часть - тороидальный многогранник .
| рассечение изображений |
|---|
Эти изображения показывают ромбикосододекаэдр (фиолетовый) и усеченный икосододекаэдр (зеленый). Если длина их ребер равна 1, расстояние между соответствующими квадратами равно φ . Остающийся после ядра тороидальный многогранник и двенадцать ротондов вырезаны. |
Ортогональные проекции [ править ]
Усеченный икосододекаэдр имеет семь специальных ортогональных проекций с центром в вершине, на трех типах ребер и трех типах граней: квадратной, шестиугольной и десятиугольной. Последние два соответствуют плоскостям Кокстера А 2 и Н 2 .
| В центре | Вершина | Край 4-6 | Край 4-10 | Край 6-10 | Квадратное лицо | Лицевой шестиугольник | Десятиугольник лица |
|---|---|---|---|---|---|---|---|
| Твердый | |||||||
| Каркас | |||||||
| Проективная симметрия | [2] + | [2] | [2] | [2] | [2] | [6] | [10] |
| Двойное изображение |
Сферические мозаики и диаграммы Шлегеля [ править ]
Усеченный икосододекаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость через стереографическую проекцию . Эта проекция является конформной , сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
Диаграммы Шлегеля аналогичны, с перспективной проекцией и прямыми краями.
| Ортографическая проекция | Стереографические проекции | ||
|---|---|---|---|
| Десятиугольник -центрированный | Шестиугольник по центру | По центру квадрата | |
Геометрические вариации [ править ]
В пределах икосаэдрической симметрии существует неограниченное количество геометрических вариаций усеченного икосододекаэдра с изогональными гранями. Усеченный додекаэдр , ромбоикосододекаэдр и усеченный икосаэдр , как вырожденные предельные случаи.
Усеченный икосододекаэдрический граф [ править ]
| Усеченный икосододекаэдрический граф | |
|---|---|
5-кратная симметрия | |
| Вершины | 120 |
| Края | 180 |
| Радиус | 15 |
| Диаметр | 15 |
| Обхват | 4 |
| Автоморфизмы | 120 (А 5 × 2) |
| Хроматическое число | 2 |
| Характеристики | Кубическая , гамильтонова , регулярная , нуль-симметричная |
| Таблица графиков и параметров | |
В математической области теории графов , A усеченного icosidodecahedral графы (или большие rhombicosidodecahedral графики ) являются графиком вершин и ребер усеченного икосододекаэдра, один из Архимеда твердых веществ . Он имеет 120 вершин и ребра 180, и является нулевым симметричным и кубическим архимедовым графом . [5]
3-х кратная симметрия | 2-х кратная симметрия |
Связанные многогранники и мозаики [ править ]
| Икосаэдр-бабочка и додекаэдр содержат две трапециевидные грани вместо квадрата. [6] | |
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [5,3] , (* 532) | [5,3] + , (532) | ||||||
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Этот многогранник можно рассматривать как член последовательности однородных узоров с фигурой вершины (4.6.2 p ) и диаграммой Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]() . При p <6 членами последовательности являются все усеченные многогранники ( зоноэдры ), показанные ниже в виде сферических мозаик. При p > 6 они представляют собой мозаики гиперболической плоскости, начиная с усеченного тригептагонального мозаичного покрытия .
. При p <6 членами последовательности являются все усеченные многогранники ( зоноэдры ), показанные ниже в виде сферических мозаик. При p > 6 они представляют собой мозаики гиперболической плоскости, начиная с усеченного тригептагонального мозаичного покрытия .
| * n 32 мутации симметрии полностью усеченных мозаик : 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. * n 32 [ n , 3] | Сферический | Евклид. | Компактная гипербола. | Paraco. | Некомпактный гиперболический | |||||||
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] | * ∞32 [∞, 3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры | ||||||||||||
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | ||||||||||||
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Заметки [ править ]
- ^ Веннингер, (модель 16, стр. 30)
- ↑ Уильямсон (Раздел 3-9, стр.94)
- ↑ Кромвель (стр.82)
- ^ Weisstein, Эрик В. "Икосаэдрическая группа" . MathWorld .
- ^ Читать, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269
- ^ Симметроэдры: многогранники от симметричного размещения правильных многоугольников Крейг С. Каплан
Ссылки [ править ]
- Веннингер, Магнус (1974), Модели многогранников , Cambridge University Press , ISBN 978-0-521-09859-5, Руководство по ремонту 0467493
- Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN 0-521-55432-2.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X.
- Cromwell, P .; Многогранники , CUP hbk (1997), pbk. (1999).
- Эрик В. Вайсштейн , Большой ромбикосододекаэдр ( архимедово твердое тело ) в MathWorld .
- Клитцинг, Ричард. «3D выпуклые равномерные многогранники x3x5x - сетка» .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. "Большой ромбикосододекаэдр" . MathWorld .
- * Вайсштейн, Эрик В. «Большой ромбикосододекаэдрический граф» . MathWorld .
- Редактируемая печатная сетка усеченного икосододекаэдра с интерактивным трехмерным изображением
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников

